Realistické RC modely

Vrtuľa a jej ťah: mýty a (overené - zmerané) fakty

Hoci sa nepovažujeme za žiadnych aerodynamických guru, tak nás taká tá „primeraná modelárska aerodynamika“ samozrejme zaujíma.

Zaujíma nás z princípu, napriek tomu, že od svojich modelov nevyžadujeme nejaké špičkové - súťažné výkony, pretože sa bytostne cítime byť modelármi rekreačnými.

A pretože sa necítime na to, aby sme všetko okolo aerodynamiky a vrtúľ, len tak - „ľavou zadnou“ zdôvodnili matematicky, nezostáva nám nič iné, ako si tieto deje na vlastnej koži odskúšať, odpozorovať, navzájom porovnať alebo priamo zmerať.

Avšak občas narazíme na tvrdenia (aj skúsených) modelárov, ktoré sú však v príkrom rozpore s našimi názormi, postrehmi, skúsenosťami alebo meraniami.

autor: Janko O.

Za tie roky modelárčenia sme došli k názoru, že asi najlepším „semeniskom“ mýtov a iných názorových nezrovnalostí je vrtuľový pohon. Je to možno tým, že prúd vzduchu v okolí vrtule, ktorý pohonná vrtuľa „rozpohybovala“, nie je (za normálnych okolností) vidno a ani „parametre“ (smer, rýchlosť, vírenie …) tohto prúdu vzduchu nie je ľahké zistiť či nebodaj kvantifikovať. Navyše existuje prekvapivo vysoké percento modelárov, ktorí zastávajú názor: „Len nič nemerať, nič nepočítať!“

A tak títo, keďže žiadne výsledky vlastných meraní (experimentov či výpočtov) nemajú, musia sa spoľahnúť na informácie, tak povediac z druhej ruky (ktoré potom bez rozmyslu viac menej len opakujú). Tie však môžu byť získané za iných podmienok a v konečnom dôsledku v tých našich rekreačno-modelárskych podmienkach sa môžu javiť trochu inak.

Jedným z takých „kľúčových“ modelárskych mýtov je ťah pohonnej jednotky. Ten môžeme chápať ako:

• ťah statický (keď sa model alebo testovaná pohonná jednotka nepohybuje)

• ťah dynamický (keď je model alebo testovaná pohonná jednotka v pohybe)

Obidva tieto ťahy sú zástancami modelárskych mýtov v podstate démonizované: ten prvý je považovaný za bezvýznamný a tým vlastne za bezcenný. A ten druhý je vraj ešte horší: jeho závislosť od rýchlosti modelu je údajne nepredvídateľná a miestami až chorá. A čo horšie: vraj ho nikto ani nepozná .

A tak je ťah (či už statický alebo dynamický) vyhlásený za tabu, takže neslobodno o ňom hovoriť nahlas a zmieňovať sa o ňom písmom, či už tým „atramentovým“ alebo elektronickým (internet), je považované za rúhačstvo . Najlepšie je vraj sklopiť hlavu a pokorne odriekavať poučky, ktoré kedysi "niekto" vyslovil .

Čo si však od snahy, aspoň trochu porozumieť „dianiu okolo točiacej sa vrtule“, sľubujeme my sami? Čo od toho očakávame?

Nuž, isto si nemyslíme, že budeme schopní na gram presne spočítať ťah tej-ktorej vrtule, pri tej-či-onej rýchlosti a z toho potom ako z kryštálovej gule „vyveštiť“ letové vlastnosti nejakého modelu.

Nie!

Skôr by sme sa chceli v tejto problematike aspoň trochu zorientovať tak, aby sme dokázali určiť (alebo aspoň odhadnúť) tendencie správania sa vrtuľového pohonu. Skrátka, aby sme dokázali povedať, že pri nejakej konkrétnej vrtuli bude s narastajúcou rýchlosťou modelu ťah klesať alebo rásť. Či tá zmena bude pozvoľná - mierna alebo strmá - razantná. Či sa v určitom rozsahu rýchlostí (alebo otáčok) môžu vyskytnúť nejaké nečakané - prekvapivé prejavy, alebo sa môžeme spoľahnúť, že všetko bude prebiehať plynule a hladko.

Na našich stránkach sme sa o ťahu zmieňovali mnohokrát, no o vzťahu medzi ťahom statickým a ťahom dynamickým pojednáva už článok „Čo robiť, aby bol model rýchly? - 1.časť – Teória“. V tomto článku sme už naozaj dosť dávno uviedli aj tento graf:

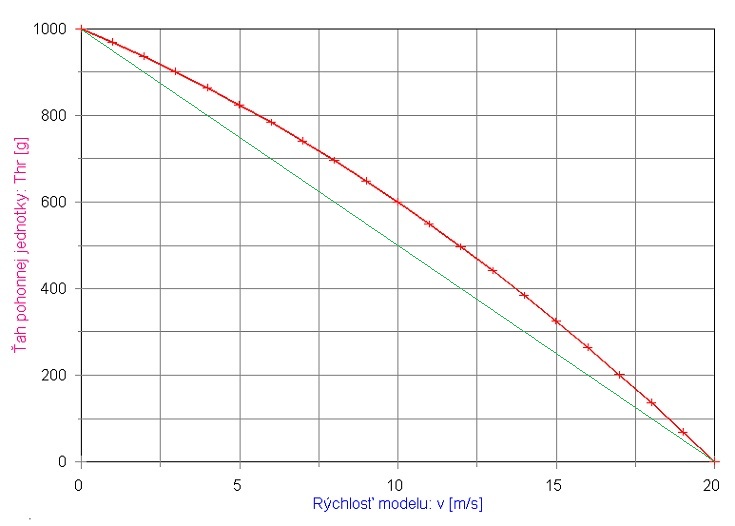
Tento graf sme si akosi intuitívne sami „vymysleli“, aby sme zdôvodnili, prečo model letí práve tou ktorou (ustálenou) rýchlosťou. Rýchlosti v₁, v₂ alebo v₃ sú stavy, kedy ťah (samozrejme že dynamický ) pohonnej jednotky bude rovnaký ako aerodynamický odpor daného modelu (tie "zakrúžkované" priesečníky krivky dynamického ťahu a krivky aerodynamického odporu).

Skutočnosti, že medzi ťahom statickým a ťahom dynamickým je (v rekreačno-modelárskej praxi, pri použití „podšrvorcových“ vrtúľ) pomerne jasná, odhadnuteľná a dokonca aj matematicky vyjadriteľná závislosť, sme pomerne nedávno venovali samostatný článok: „Aký je ťah elektro-pohonnej jednotky počas letu modelu?“. Na podporu tohto tvrdenia tu uvádzame aj niekoľko grafov, ktoré túto závislosť názorne zobrazujú. Tu je jeden z nich (tá modrá krivka):

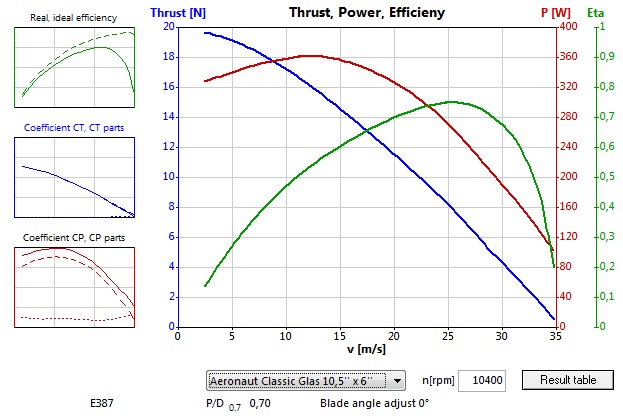
V podstate rovnakú závislosť dynamického ťahu od rýchlosti (lietadla, modelu, pohonnej jednotky) v grafe s názvom „Aerodynamické charakteristiky vrtule“ uvádza vo svojom článku „Statický a využitelný tah vrtulové pohonné jednotky“ aj pán Jaroslav Lněnička:

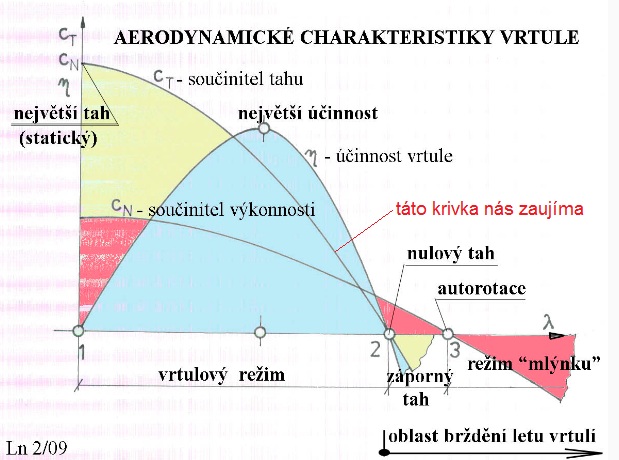
Obrázok sme nepoužili celý, ale len jeho časť, týkajúcu sa danej problematiky a (červeným písmom) sme ukázali na krivku, ktorá nás na celom grafe najviac zaujíma.
 

Z uvedených podkladov vyplýva, že medzi statickým a dynamickým ťahom bežných rekreačno-modelárskych (teda tzv. podštvorcových) vrtúľ je pomerne pevný a (krivkami grafov) predvídateľný vzťah, bez nejakých „excesov“ v podobe náhlych a nečakaných „hrbov“ alebo prepadov. Navyše, tak ako je to spomínané v článku „Aký je ťah elektro-pohonnej jednotky počas letu modelu?“, je možné zo statického ťahu, stúpania vrtule a otáčok motora pomerne presne (s nepresnosťou nepresahujúcou 5 až 10%) stanoviť dynamický ťah danej vrtule pri danej rýchlosti modelu.

Pri našich experimentoch a ani v serióznej literatúre sme nenarazili na tvrdenie (mýtus), že ťah podštvorcovej vrtule stojaceho (nepohybujúceho sa) modelu je pomerne malý a až po dosiahnutí určitej rýchlosti sa vrtuľa „chytí“ a začne riadne ťahať. Tak ako to tvrdí jeden naozaj skúsený modelár:

„Pro příklad - vrtule 250 má obvod 785. Když ji roztočíš na 15 000 otáček, je to 250 za vteřinu. Konce pak mají 196 m/s. To už jsou dvě třetiny rychlosti zvuku. Větší průměr nebo točky už nemají význam, roste odpor.

Pokud by model s takovou vrtulí měl létat kolem stovky, je to asi 30 m/s, tedy na 12 cm na otáčku vrtule. Ta by tedy měla mít stoupání cca. 150 -180.

Když bude mít 100, bude při té rychlosti a otáčkách brzdit. Naopak, jako statická při nulové rychlosti letu je to pak křídlo s rychlostí 700 km/h a náběhem přes 7°, tedy s urvaným prouděním, co sice trochu táhne, ale hlavně míchá vzduch.

A někde mezi tím, tam kde list vrtule bude mít optimální náběh, bude mít vrtule nejlepší tah. A odpovídající rychlostí by měl model letět a v takové rychlosti by i vrtule měly být měřena, pokud z toho mají vypadnou užitečná čísla.

Mezi statickým a dynamickým tahem není žádný matematický vztah. Podobně jako u křídla. Tam taky ze vztlaku při urvaném proudění nemůžeš nijak vypočítat vztlak v optimálním stavu.“

Nie že by sme s jeho tvrdeniami principiálne vo všetkom nesúhlasili, skôr nám vŕtali v hlave tie vety, ktoré sme podtrhli.

Nechcelo sa nám veriť, že by bol vzduch vrtuľou stojaceho (nepohybujúceho sa) modelu urýchlený len tak málo, že by uhol nábehu listov vrtule (voči prúdiacemu vzduchu) bol neuveriteľných 7°. A tak sme opäť zažili naše obľúbené Déjà vu. Skrátka: skúsený modelár neochvejne tvrdí niečo iné, ako dokazujú naše skúsenosti, postrehy alebo dokumentačné podklady. A tak sme opäť zapochybovali (sami o sebe ) a povedali si: „Čo ak má pravdu?“ A opäť sme došli k rovnakému rozhodnutiu: najlepšie bude to zmerať.

Na tento experiment sme si vybrali model Partenavia P-66 Oscar:

Jeden z dôvodov je ten, že má značkovú vrtuľu (APC 17x8 E), jeho telemetria je vybavená otáčkomerom a je dostatočne veľký, aby sme aj bežným anemometrom dokázali zmerať rýchlosť prúdu vzduchu v 75% priemeru vrtule. Ako anemometer (prístroj na meranie rýchlosti vetra) sme použili tento:

ktorý má až do rýchlosti 90km/h nepresnosť merania menšiu ako 5%. To nám pre naše orientačné experimentovanie bohato stačí.

Model sme vyniesli na terasu pri našom dome, zapli batériu a pomocou telemetrie sme postupne nastavili otáčky motora: 3000/min, 4000/min, 5000/min a 6000/min. Súčasne sme vhodne „situovali“ anemometer:

Keď mal motor požadované otáčky, odčítali sme hodnotu rýchlosti „vetra“, ktorý točiaca sa vrtuľa spôsobovala.

Z nameraných výsledkov sme zostali úplne PAF :

• pri 3000 otáčkach za minútu (50 otáčok za sekundu) bola nameraná rýchlosť prúdu vzduchu 9,8 m/s.

• pri 4000 otáčkach za minútu (66,6 otáčok za sekundu) bola nameraná rýchlosť prúdu vzduchu 13,2 m/s.

• pri 5000 otáčkach za minútu (83,3 otáčok za sekundu) bola nameraná rýchlosť prúdu vzduchu 16,7 m/s.

• pri 6000 otáčkach za minútu (100 otáčok za sekundu) bola nameraná rýchlosť prúdu vzduchu 20 m/s.

Sme si vedomí toho, že hoci sme miesto merania starostlivo vybrali tak, aby vplyvom kapotáže či kabíny boli prúdnice zhustené čo najmenej, že namerané hodnoty rýchlosti budú o pár percent vyššie ako by mali správne byť. Ale až takéto hodnoty (fakticky zhodné s teoretickými) sme nečakali: pretože v duchu tvrdenia onoho vyššie citovaného modelára mali byť asi tretinové.

Prekvapivosť nameraných výsledkov najlepšie vyznie, keď si ich porovnáme s hodnotami teoretickými, ktoré vychádzajú zo stúpania vrtule a jej otáčok, pri zanedbaní tzv. sklzu.

Teoreticky by pri nulovom sklze mali byť rýchlosti prúdu vzduchu nasledujúce:

• pri 3000 otáčkach za minútu (50 otáčok za sekundu) by mala byť rýchlosť prúdu vzduchu 10,1 m/s.

• pri 4000 otáčkach za minútu (66,6 otáčok za sekundu) by mala byť rýchlosť prúdu vzduchu 13,5 m/s.

• pri 5000 otáčkach za minútu (83,3 otáčok za sekundu) by mala byť rýchlosť prúdu vzduchu 16,9 m/s.

• pri 6000 otáčkach za minútu (100 otáčok za sekundu) by mala byť rýchlosť prúdu vzduchu 20,3 m/s.

Aby sme mohli posúdiť, či je možné, aby za daných podmienok bol nábeh vrtuľového listu voči okolitému vzduchu spomínaných viac ako 7°, rozhodli sme sa vypočítať uhol nábehu vrtuľového listu našej vrtule. Vyšlo nám: asi 10,7°. Okrem toho sme sa rozhodli to zmerať. Urobili sme si špeciálny prípravok, ktorý sme nazvali: čínske špáradlo . Prilepili sme ho (čínskym gumovitým lepidlom) v tej správnej polohe na vrtuľu a odfotili.

Potom sme v kľude pri počítači na monitore pomerali ten správny uhol (nábehu), ale pre istotu aj tie správne odvesny, na kalkulačke využili funkciu arkustangens a dostali v podstate totožnú hodnotu: cca 10,5 stupňa.

A bolo to jasné! Ak by sa vrtuľa s uhlom nábehu necelých 11° mala „zavŕtavať“ do vzduchu s uhlom nábehu vyše 7°, tak by sa prúd vzduchu vrtuľou urýchlený, mal pohybovať oveľa-oveľa pomalšie, než ako sme namerali. Zhruba tretinovou rýchlosťou, tak ako sme to spomenuli už skôr.

Možno sa modelárom - mýtotvorcom vryla do podvedomia charakteristika nadštvorcových vrtúľ (modrá krivka), ktorá môže vyzerať napr. aj takto:

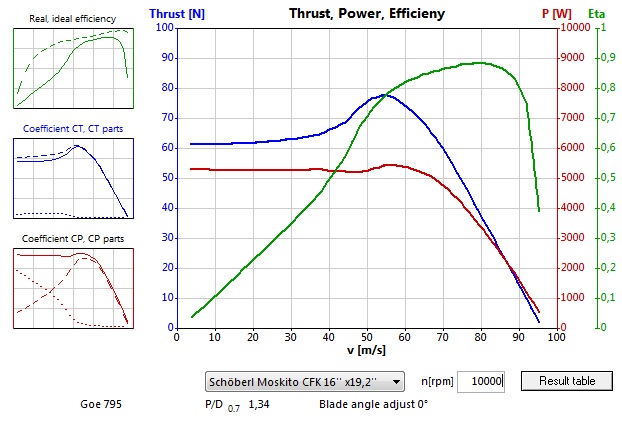
Tu naozaj roztočená vrtuľa stojaceho modelu má menší ťah ako keď sa vrtuľa (lietadlo, model) pohybuje určitou rýchlosťou. Treba však podotknúť, že vtedy je (statický) ťah len o trochu (napr. o 20%) nižší ako (dynamický) ťah v jeho maxime, takže tvrdenie, že taká vrtuľa v statickom režime síce TROCHU ťahá, ale hlavne mieša vzduch, je prinajmenšom prehnané. Tiež si treba všimnúť, že je to vrtuľa už dosť nadštvorcová (16 x 19,2), zatiaľčo vrtule mierne nadštvorcové, ako napríklad APC 7x8 S, majú takú zvláštnu, povedali by sme vzácne „vyrovnanú“ charakteristiku:

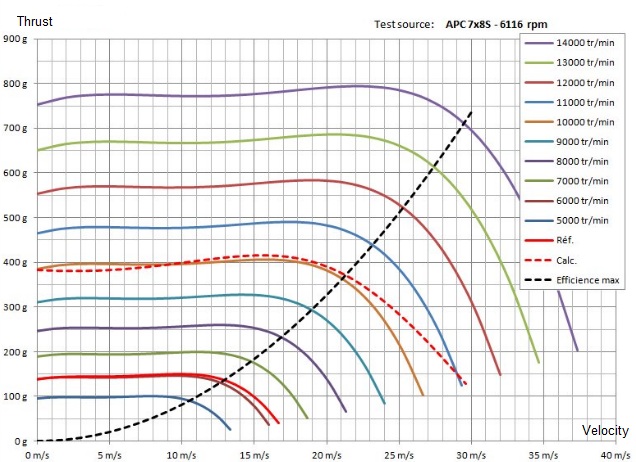
Vrtule, ktoré sú nadštvorcové viac, majú na charakteristike hrb (tak ako nad týmto grafom zobrazená Schöberl Moskito CFK 16 x 19,2), vrtule štvorcové skôr nie. A vrtule podštvorcové majú charakteristiku peknú – monotónnu; to znamená, že s narastajúcou rýchlosťou dynamický ťah stále (nudne a monotónne) len klesá a nikdy sa nestane, že by pri nejakej rýchlosti zrazu nečakane a prekvapivo „povyskočil“.

Z toho vyplýva, že (podštvorcové) vrtule, ktoré používajú bežní rekreační modelári, majú (ako my hovoríme) slušne vychovanú charakteristiku, ktorá dokonca pre tzv. polštvorcové vrtule (napr. 8x4) nie je ďaleko od lineárnej závislosti:

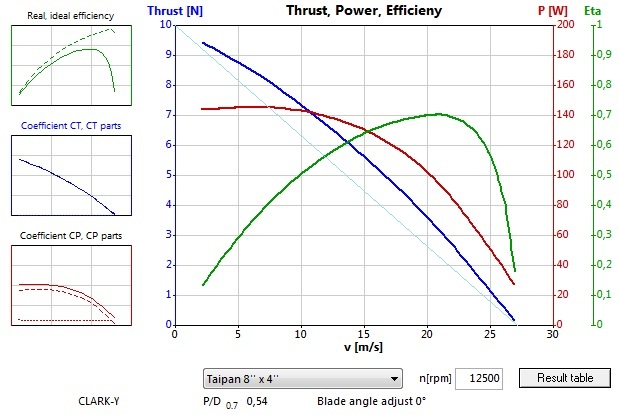
 Matematicky namodelovaný, pomocou vzťahu:

Ťah_Dynamický = Ťah_Statický – ((Rýchlosť + Koeficient₁)² - Koeficient₂)

tvar krivky ťahu podštvorcovej vrtule.

Ich ťah (ktorý je najprv maximálny = statický ťah) s narastajúcou rýchlosťou postupne a plynule klesá bez akýchkoľvek záludností, až pri určitej rýchlosti (v_pitch, ktorá je daná stúpaním vrtule a jej otáčkami) bude nulový.

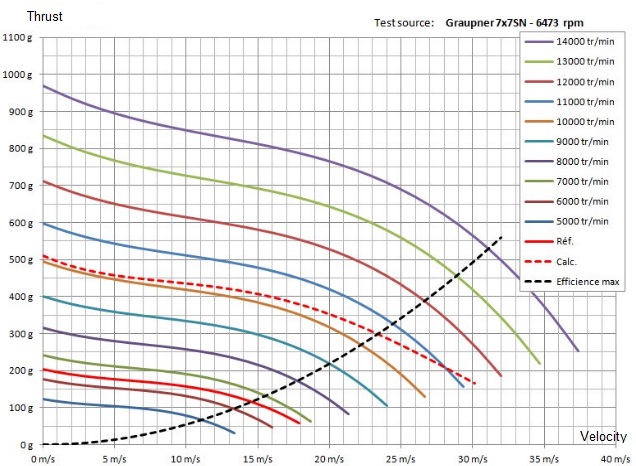
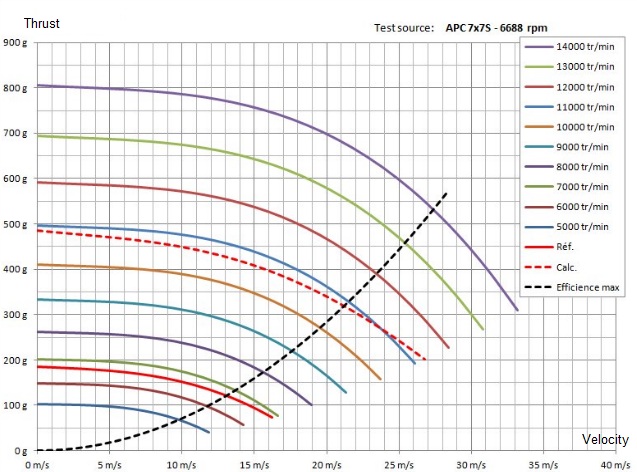
Na porovnanie uvedieme niekoľko aerodynamických charakteristík vrtúľ rovnakého priemeru a rovnakého ale aj rôzneho stúpania. V každom grafe je vicero kriviek - pre rôzne otáčky vrtule.

Švorcová vrtuľa (square propeller) Graupner 7x7 Super Nylon:

Švorcová vrtuľa (square propeller) APC 7x7 Sport:

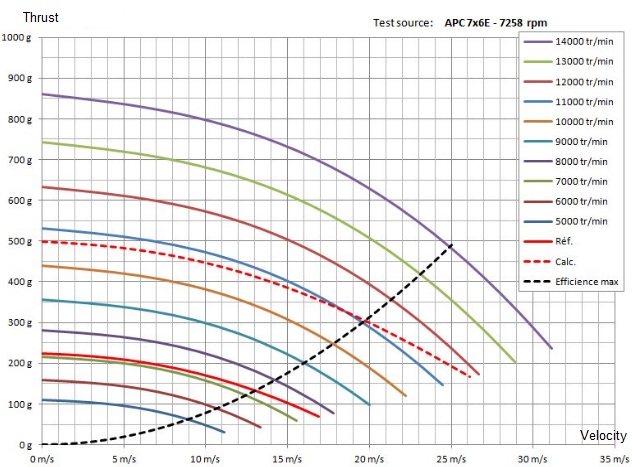
Podšvorcová vrtuľa APC 7x6 E:

Podšvorcová vrtuľa APC 7x4 E: 

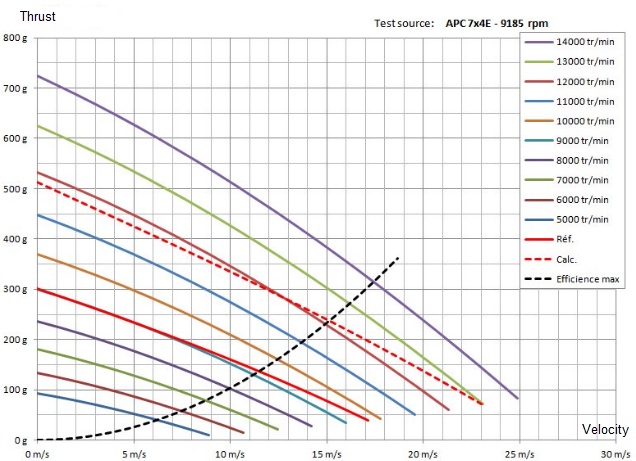
Všimnite si, že čím je stúpanie danej vrtule menšie, tým je tendencia klesania dynamického ťahu jednoznačnejšia - jednoduchšia - predvídateľnejšia. Avšak ani u štvorcových vrtúľ nie je statický ťah nižší ako ťah pri narastajúcej rýchlosti modelu. A o "chorých" tvaroch priebehov v blízkosti nulových dopredných rýchlostí nemôže byť ani reči.

Na záver niečo z našich (praktických) skúseností, ako je to so vzťahom statického a dynamického ťahu a ako je to s „chorosťou“ charakteristiky vrtule:

Posledné asi dva roky sa intenzívne venujeme konvertoplánom. Ak niekto nemá rád konvertoplány, tak si miesto nich môže "dosadiť" vrtuľníky, koptéry, alebo aspoň akrobatický model, visiaci na vrtuli. Ak niekto povie, že aj tu nám je znalosť statického ťahu na nič, tak potom nemá zmysel, aby sme s ním strácali čas.

Všetky tieto zariadenia však len nehybne nevisia, ale sa do visu z pohybu musia aj nejako dostať, rovnako ako sa musia dostať z visu do pohybu. Inými slovami: tu sa plynule prechádza z ťahu dynamického do ťahu statického a potom zase do ťahu dynamického. Všetky tieto prechody (či už stúpanie, alebo dopredný let) sú úplne plynulé a hladké. Ak by priebeh dynamického ťahu v okolí malých dopredných rýchlostí bol nejako "chorý", tak by tieto prechody nemohli byť plynulé a hladké.

Komentáre: 5

.:. J O.

Vlado,
vďaka za pochvalu aj za podporu .

Odpoveď | 2020-10-06 08:13:57

Meno
Web
Mail
Kontrola	Zadajte číslo päť
Text
	Tučné | Podrazené | Kurzíva  | zdroják | odkaz