Sú ťažšie modely skutočne rýchlejšie?
Na tomto základe sa s určitou mierou bojazlivosti (spolu s mojim bratom Miroslavom) pýtame: "Je ťažší model skutočne rýchlejší ako taký istý model s nižšou hmotnosťou?"
A odpoveď nemusí byť vôbec taká, akú by mnohí, tak akosi samozrejme očakávali.
autor: Janko O.
Medzi modelármi je pomerne zaužívaný názor, že ťažký model = rýchly model.
Sme si vedomí skutočnosti, že týmto sa dostávame trochu na "tenký ľad" teórie, pretože mnohé nasledujúce tvrdenia nebudú podložené praktickými meraniami (ako to máme najradšej), ale na pomoc sme si vzali "mocného" spojenca: Informácie získané z mnohých diel "Učiteľa česko-slovenských modelárskych národov" pána Jaroslava Lněničku. 
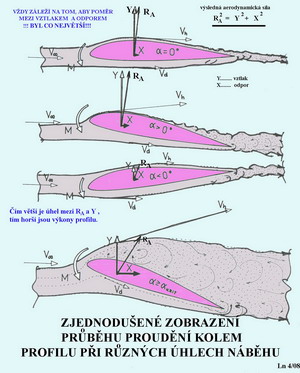
Takže, ak by sme mali za seba odpovedať na otázku, ktorá je položená v názve tohoto článku, odpovedali by sme trochu alibisticky: "Áno aj nie, ako kedy". Takáto odpoveď nie je súca ani na to, aby sa strčila za klobúk, ale i tak je pravdivá. Kľúč je skrytý v tom "ako kedy". Treba rozlíšiť tri rôzne fázy letu:
* bežné poletovanie,
* let minimálnou dosiahnuteľnou rýchlosťou a
* let maximálnou dosiahnuteľnou rýchlosťou.
V úvode tohoto odstavca chceme vyjadriť názor, že slovná asociácia: ťažký model = rýchly model, by mala byť aj opačná: rýchly model = ťažký model. Ak v tom nie je vidieť rozdiel, chceme zdôrazniť, že ľavá strana rovnice je príčina a pravá je následok. Takže za to, že ťažké modely majú povesť rýchlych modelov, môže skutočnosť, že do rýchleho modelu zamontujeme úmyselne výkonnejšiu pohonnú jednotku, ktorá býva spravidla aj ťažšia.
A keďže výkonnejšia pohonná jednotka bude mať aj vyššiu spotrebu, zamontujeme do modelu objemnejšiu nádrž s väčším množstvom paliva, alebo pohonnú jednotku musíme poháňať batériou s väčšou kapacitou, ktorá spravidla býva aj ťažšia. Druhou možnosťou, ako ťažké modely prišli k povesti rýchlych, je fakt, že ťažší model, aby sa udržal vo vodorovnom lete, musí vyvodzovať väčší vztlak. A to sa dá dosiahnuť buď väčším uhlom nábehu krídla, ktorý však spôsobuje vyšší koeficient odporu vzduchu (čiže spomaľuje), alebo vyššou rýchlosťou letu.
Obzvlášť do pozornosti dávame veľkosti plôch, na obrázku označené ako "Ztracená energie proudu"
A máme zdôvodnenie, prečo ťažšie modely "bežne poletujú" rýchlejšie.
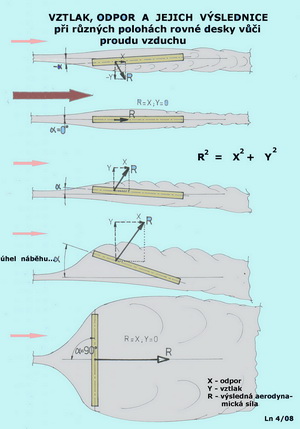
Ako je to s minimálnou dosiahnuteľnou rýchlosťou? Ak pominieme modely, ktoré "visia" na motore alebo na turbíne (krásna predstava 
), opäť musíme vziať v úvahu, že vyššia hmotnosť musí byť kompenzovaná väčším vztlakom. A keďže uhol nábehu nemôžeme zvyšovať do neúnosných hodnôt, pretože by došlo k odtrhnutiu prúdnic okolo profilu a k pádu modelu, nezostáva nič iné, ako opäť zvýšiť rýchlosť. Z toho vyplýva, že ťažšie modely majú vyššiu minimálnu dosiahnuteľnú rýchlosť. Ani nevieme, či je to víťazstvo alebo prehra. Ale tí, čo s takýmto modelom chcú hladko pristáť, o tom vedia svoje.
A teraz to najdôležitejšie - maximálna dosiahnuteľná rýchlosť. Predstavme si: dva úplne rovnaké modely, s rovnakým výkonom, letia vedľa seba na plný plyn. Ale jeden z nich je ťažší. A aby sa udržal vo vodorovnom lete, musí vyvodzovať väčší vztlak (fajn, už to opakujeme tretí krát). Zvýšiť rýchlosť nemôže; plyn už je naplno. Takže na kompenzovanie vyššej hmotnosti mu nezostáva nič iné, ako zväčšiť vztlak zvýšením uhlu nábehu. Ale ten predsa zvyšuje koeficient odporu vzduchu, čiže brzdí (viď poláry profilov, určených pre rýchle modely). Predchádzajúca veta asi nepoteší milovníkov ťažkých modelov, ale záver je jasný:
Ťažšie modely majú maximálnu dosiahnuteľnú rýchlosť vo vodorovnom lete nižšiu ako modely ľahšie.
A na záver spomeňme rozsah rýchlostí, teda rozdiel (alebo aj pomer) maximálnej a minimálnej rýchlosti letu modelu. Už asi tušíte aký bude záver:
Čím je model ťažší, tým má menší rozsah rýchlostí.
Pretože minimálna rýchlosť modelu s jeho váhou stúpa a maximálna klesá: približujú sa k sebe.
Možno ste už videli modelára, ktorý sa pokúšal lietať so skutočne ťažkým modelom: niektorým sa to (na chvíľu) aj podarí. V extrémnom prípade sa môže stať, že je model taký ťažký, že letí LEN na plný plyn. Vtedy je jeho minimálna letová rýchlosť prakticky rovnaká ako rýchlosť maximálna a rozsah rýchlostí = nula.
Na obrázku je zreteľne vidno, že SR-71, ktorý má väčšie plošné zaťaženie a je určený pre oveľa väčšie rýchlosti (až Mach 3), musí pri danej rýchlosti letieť pod väčším uhlom nábehu, ako jeho tanker
Aby sme zmiernili duševnú traumu, ktorú predchádzajúci odstavec spôsobil niektorým modelárom, treba priznať, že ťažšie modely majú aj výhody.
Aj na tomto obrázku vidno, že SR-71, pre ktorý je táto "spoločná" rýchlosť dosť nízka, letí pod väčším uhlom nábehu, ako tankovacie lietadlo.
Predovšetkým je to, vďaka vačším zotrvačným hmotám, vyššia stabilita letu. Chápané v zmysle toho, že takýto model je obzvlášť v nárazovom vetre oveľa lepšie ovládateľný a nestáva sa, na rozdiel od väčšiny ľahkých modelov, len úbohou hračkou v osídlach tohoto zlomyselníka.
Poznámka:
Schémy sú použité z Akademie letectví , kde autorom je pán Jaroslav Lněnička -
www.airspace.cz/akademie/rocnik/2008/08/profily.php
a
www.airspace.cz/akademie/rocnik/2008/07/profily.php
<Staršie | tento článok | Novšie>
Napísané: 6. 2. 2022, 09:36 | Prečítané: 11022x | Kategórie: Lietanie | Napísal: admin |
Komentáre: 10
niekedy by som privital nejaky clanok o teme, ktoru nemozem dohladat na forach:
tak ako mame skutocnu teplotu a pocitovu, myslim ze existuje nieco take ako pocitova rychlost (zalozena na velkosti modelu) a skutocna rychlost. Vidim to na rychlosti mojho Mirage, kde sa mi nezda velka a moj najmensi model Parkzone Micro Mustang, kde sa mi zda dost velka, vzhladom na male rozmery. A este jedna tema nad ktorou dumam, maketova ryclost. Ako vydelit rychlost makety vzhladom na mierku, aby sme dosiahli maketovu rychlost predlohy. Niekedy vidim lietat WW2 polomakety ako akrobaty, co sa mi zda trocha divne. Inac dobry WEB chalani, len tak dalej
ďakujem za tému, keď sa trochu časovo uvolním (musím chodiť aj do práce a navyše doma nemám internet) nejakú takú úvahu by bolo dobré napísať. Ale len tak na rýchlu orientáciu, myslím, že pocitová a maketová rýchlosť budú veľmi blízke, ak nie totožné. Ide o to, že skutočné lietadlo urazí vzdialenosť, rovnajúcu sa jeho dĺžke, za nejaký čas. Ak aj model urazí vzdialenosť, rovnajúcu sa jeho dĺžke, za ten istý čas ako skutočné lietadlo, budeš mať pocit maketovosti. Pri snímaní kamerou jedného aj druhého prípadu, nebude rozoznateľné, či sleduješ model, alebo skutočné lietadlo.
Janko
Ako vydelit rychlost predlohy vzhladom na mierku, aby sme dosiahli maketovu rychlost modelu.
rýchlosť predlohy vydel mierkou zmenšenia modelu a dostaneš maketovú rýchlosť. Napr.: model je 5 krát menší ako skutočné lietadlo - predloha, takže rýchlosť modelu by mala byť 5 krát menšia.
na okraj >"Je ťažší model skutočne rýchlejší ako taký istý model s vyššou hmotnosťou?"
zrejme predposledne slovo malo byt nizsou...
sympaticke je ze aj autor je len clovek...drzim palce, nelucim sa, este to tu zdaleka nemam cele prebrowsovane...
pozn. maximální dosažitelná rychlost ve vodorovném letu je vždy nižší, než maximální dosažitelná rychlost.
"Medzi modelármi je všeobecne zaužívaný názor, že ťažký model = rýchly model."
Toto ste zjavne zle pochopili. Tento výrok znamená presne to na čo ste došli bádaním, že sa zvýši jeho pádová rýchlosť, ktorá je od plošného zaťaženia (+iných serepetičiek) závislá.
Tým pádom aj keď sa vraví že ten model bude "raketa" model poletí len tak rýchlo ako mu to umožní vrtuľa (otáčky a stúpanie). Ale bude nutné lietať na väčšej rýchlosti práve kôli tým prúdniciam a uhlu nábehu.
Takže celá pointa tohoto inak poučného článku pre začiatočníkov a mierne pokročilých je trošku mimo....
Ale keď sa dobre poobzeráme vôkol, po kopcoch a lúkach, čo vidíme: možno to isté, ale skôr ešte slabšie modelárske vybavenie.
Jeden článok na tejto Web stránke pojednáva o pravidle 80/20. A my naozaj patríme do tej skupiny 80. Čo tým myslím? Že 80% modelárov má zhruba to, čo my. A tento web je vlastne určený pre nich.
Nemyslím, že by našu Web stránku (pravidelne) navštevovali špičkoví modelári. Zriedka-ktorý článok by ich zaujal, ak vôbec nejaký. Ale nám to nevadí a navyše by asi pôsobilo trochu kŕčovito, keby niekoľko (ak zarátam aj našich externých autorov článkov) priemerných modelárov niečo elementárne vysvetlovalo nejakým skúseným modelárom, čo patria medzi európsku či svetovú špičku.
A teraz odpoveď na otázku: "Rád by som vedel odkial máte (š) názor že ťažký model je rýchlejší ako ten istý ľahší teda s menším plošným zaťažením?"
Nuž, často to počujeme na kopci, či na lúke, medzi amatérskymi modelármi: "To je ťažký model, ten poletí vyššou maximálkou ako tie, čo ste minule merali."
Bereme to tak, že pre novorodenca je aj ten najstarší vtip nový.
Môžeme ich vysmiať, môžeme z nich priamo na lúke urobiť dementov, alebo im to môžeme vysvetliť. Ja osobne som v škole nemal rád, keď nám fyzikár kázal naučiť sa, že sila má skratku F, rýchlosť má skratku V, dĺžka má skratku L atď. Oveľa lepšie znesiem, keď mi niekto povie, že sila má skratku F od anglického Force, rýchlosť V od velocity a L od lenght.
Možno je náš spôsob vysvetlovania zdĺhavý a pre niekoho ťažkopádny, ale možno to ani inak nevieme.
Na druhú stranu nás poteší, keď ten NÁŠ spôsob vysvetlovania niekto ocení, tak ako to napísal Martin:
Pre autorov webu :
" obliect problematiku elektroniky do kabatu jednoduchosti tak, aby to pochopil kazdy a k tomu s pouzitim "primitivnych" (prosim to neni urazka - slovo primitivne je pouzite LEN v zmysle technickej jednoduchosti prevedenia jednotlivych merani ) je niekedy dost velky problem ". Je vela stranok pojednavajucich o RC elektronike, ale velmi malo stranok ktore to VEDIA vysvetlit - jednoducho - rukolapne - meranie - obrazok - vysvetlenie - zaver
KLOBUK DOLE a moj obdiv pani !!!!
Originál je tu: odkaz
Na vyvratenie komentarov, ze jedna lipolka je lepsia a preto model leti rychlejsie, som v elektrodielni zhotovyl 30A zataz a meral. Po 1 minute som nameral minimalny rozdiel 0,14V medzi sadami. Aj mna to velmi prekvapilo, ale je to tym, ze 1300-vka je tvrdsia.
Pozn: len tak pre zaujimavost, tazisko s 1800-vkou mam pred krydlom :D a z 1300 -vkou presne na nabezke. Pred prvym letom som mal velke obavy, ale bol som milo prekvapeny. Pylonak leti ako po "kolajniciach", vietor mu zacne vadit az ked fuka nad 10m/s, ale zas povetre je este rychlejsi...
Toto je okresany clanok, pri povodnom mi vypisalo chybove hlasenie "chyba pri autorizacii"
Pridaj komentár
- Pre odoslanie správy môžete aj použiť klávesovoú skratku Alt+S. (Podporujú len niektoré prehliadače)
- HTML znaky budú prevedené na entity.
- Vyjadrujte sa tu ako doma, aby sme vedeli ako to u Vás vypadá.
- Odkazy začínajúce http:// budú automaticky prevedené na odkazy , nepoužívajte však v jednom príspevku viac ako 3 - to robia len spam roboti:-)